Tips from the Experts

Raiders of the Lost ArXiv: Citation Searching in a Disciplinary Repository

John J. Meier
Science Librarian
The Pennsylvania State University
University Park, Pennsylvania
jjm38@psu.edu

Librarians are often called upon to perform citation searches of faculty publications in order to support their promotion and tenure cases. The methods over the years have gone from using print indexes to online searching and from using one source, such as ISI's Science Citation Index (Web of Science), to multiple sources including Google Scholar and Scopus. Many subject databases such as MathSciNet from the American Mathematical Society (AMS) also now provide citation counts using the data available in their systems.

In discussing with a faculty member in the mathematics department which system to search we decided to search as many as possible in order to leverage the strengths of each system. For example, ISI's system is still the most respected while Google Scholar is considered to include the most results. Though Google Scholar indexes the arXiv http://arxiv.org/ (2014), a preprint server for Physics and Math along with some related subject areas, we wondered if searching within arXiv itself would yield additional citations.

We decided to use the "experimental full text search" feature on the advanced searching page (http://arxiv.org/find). There were two approaches to use, the first was to retrieve all papers that cited the author by using the author's name as formatted for citation (eg, "K. Schwede"). This would require only one search per person with the results containing all papers mentioning the author. The alternative is to search by paper name (eg, "Test ideals in non-Q-Gorenstein rings") and repeat this process for all papers by the author. Both searches can take a while to complete.

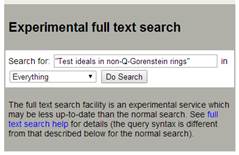
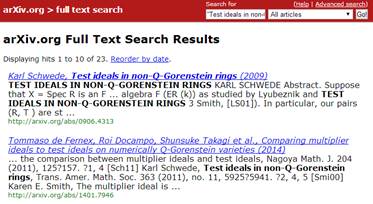
The former approach was used by the mathematics faculty member in order to create a database of citations of his work. Since it requires deduplication and sorting, this method is labor intensive at the beginning but allows for a greater level of accuracy and also reuse of the data. Database queries can be made on the system in order to remove self-citations and duplicates.

I used the latter approach to find the number of citations for the ten most highly cited papers as ranked by Google Scholar, for which I had also gathered citation counts from ISI Web of Science. I ran three trials for separate articles, disregarding the article itself in the arXiv searches.

After examining the results in detail for "Test ideals in non-Q-Gorenstein rings" - full results available from ScholarSphere (Meier 2014) - I discovered that the three additional Google Scholar citations over arXiv were all duplicates. Therefore, the arXiv search was more accurate without missing any other citations. The six results from Web of Science were also found in both the Google Scholar and arXiv results; in fact due to a recent partnership (Thomson Reuters 2013) Web of Science results are linked to Google Scholar. This first trial did not reveal any additional citations from arXiv over Google Scholar. This was expected since Google Scholar indexes arXiv, but arXiv is limited to papers in its repository. These included self-citations, which were tagged in case they needed to be removed later.

However, in two of my other searches in arXiv I found an additional citation in arXiv that was not in Google Scholar in addition to some citations in Google Scholar that were not in arXiv. These were not the most recently indexed papers, which would have indicated a time delay of indexing. It seems that we cannot take for granted that Google Scholar is finding all citations from the arXiv even though it indexes these papers. The other astonishing fact I discovered is the impact of a paper not yet published, particularly in some areas of mathematics, can be so far reaching. Thus we cannot neglect this data source when attempting to quantify the impact of a scholarly work.

I would like to acknowledge the assistance of Karl Schwede with this project.

References

ArXiv.org E-print archive. [Internet]. [Updated 2014 Apr 15]. Ithaca (NY): Cornell University Libraries. Available from: http://arxiv.org/

Meier, J.J. 2014. Citation Searching on The ArXiv. [Uploaded 2014 Apr 24]. Available from: https://scholarsphere.psu.edu/files/6395wb113

Thomson-Reuters. Web of Science & Google Scholar. [Internet]. [Updated 2014 Mar 25]. Available from: http://wokinfo.com/googlescholar/

This work is licensed under a Creative Commons Attribution 4.0 International License.